[DE] Shellsort Laufzeitanalyse

Donald Shell stellt 1959 in [📖She59] einen Sortieralgorithmus vor, der später nach ihm benannt wird: Shellsort.
Die in dem Algorithmus verwendete Sortiermethode ist auch bekannt als Sortieren mit abnehmenden Inkrementen [📖OW17b, p. 88], das Verfahren ist eine Variation von Insertion Sort:

[Shellsort] uses insertion sort on periodic subarrays of the input to produce a faster sorting algorithm. [📖CL22, p. 48]

In der vorliegenden Implementierung (siehe Listing 1) werden $t = log_2(n)$ Inkremente¹ $h_t$² der Form $\lfloor {\frac{n}{2^i}} \rfloor$ verwendet, um $lg(n)$ $h$-sortierte Folgen zu erzeugen. Im letzten Schritt sortiert der Algorithmus dann in $h_1$ die Schlüssel mit Abstand=$1$.

Die Effizienz des Sortierverfahrens ist stark abhängig von $h$: So zeigt Knuth, dass $O(n^{\frac{3}{2}})$ gilt, wenn für $h$ gilt: $h_s = 2^{s+1} - 1$ mit $0 \leq s < t = \lfloor{lg(n)} \rfloor$ (vgl. [📖Knu97c, p. 91]³. In unserem Fall können wir von $O(n^2)$ ausgehen.

Anzahl der Aufrufe für Feldvergleiche

Gesucht ist die Anzahl der zwischen zwei Feldelementen gemachte Vergleiche für große randomisierte Felder. Wir vermuten hierfür einen Wert zwischen $O(n\ lg\ n)$ und $O(n^2)$,

Um die Aufrufe der Feldvergleiche zu zählen, kann wie in Listing 1 eine Zählvariable $c3$ eingesetzt wird, die jeden Aufruf über ein increment protokolliert.

Listing 1: Zur Protokollierung der Aufrufe können in dem Code Zählvariablen eingesetzt werden (c1, ... ,c4).

while (distanz > 0) {
    c1++;
    for (i = distanz; i < feld.length; i++) {
        j = i - distanz;
        c2++;
        while (j >= 0) {
            c3++;
            if (feld[j] > feld[j + distanz]) {
                c4++;
                swap(feld, j, j+distanz);
                j = j - distanz;
            } else {
                j =-1;
            }
        }
    }
    distanz = distanz / 2;
}

Zur Bestimmung von $c3$ können randomisierte Felder erzeugt werden, wie es der Test-Code in Listing 2 demonstriert. Dann wird überprüft, in welchen Bereichen sich $c3$ bewegt. Da jeder auf Vergleichsoperationen basierende Sortieralgorithmus zu der Laufzeitklasse $\Omega(n\ log\ n)$ gehört, kann im Mittel $c3 \geq n\ log\ n$ angenommen werden:

Jedes allgemeine Sortierverfahren benötigt zum Sortieren von N verschiedenen Schlüsseln sowohl im schlechtesten Fall als auch im Mittel wenigstens $\Omega(N\ log\ N)$ Schlüsselvergleiche.

[📖OW17b, p. 154]

Allerdings wird $n^{1.3}$ ab $n=982$ schneller wachsen als $n\ log\ n$ (siehe Abbildung 1), was in der Auswertung berücksichtigt werden muss. Sonst könnte man fälschlicherweise folgern, das in dem geg. Fall die Laufzeit im Durchschnitt $n\ log\ n$ beträgt.

Listing 2: Code zum Erzeugen randomisierter Felder zum Testen von Shellsort.

int epochs = 2000;
while(epochs-- >= 0) {
    int[] tests = new int[]{10, 100, 1000, 100_000, 1_000_000};
    java.util.Random r = new java.util.Random();
    for (int i = 0; i < tests.length; i++) {
        int l = tests[i];
        int[] arr = new int[l];

        for (int j = l; j > 0; j--) {
            arr[l - j] = r.nextInt(l + 1);
        }

        ShellSort.sort(Arrays.copyOfRange(arr, 0, arr.length));
    }
}

info

Mit einem Wert von $100$ für die Epochen und einer Feldgröße von $2.000.000$ liefert der Test in Listing 2 folgende Ausgabe:

$nlgn < n^{1.3} < x < n^2: 74$
$nlgn < x < n^{1.3}: 26$

^{Figure 1 Ab n=982 wächst n(4/3) schneller al n log n.}

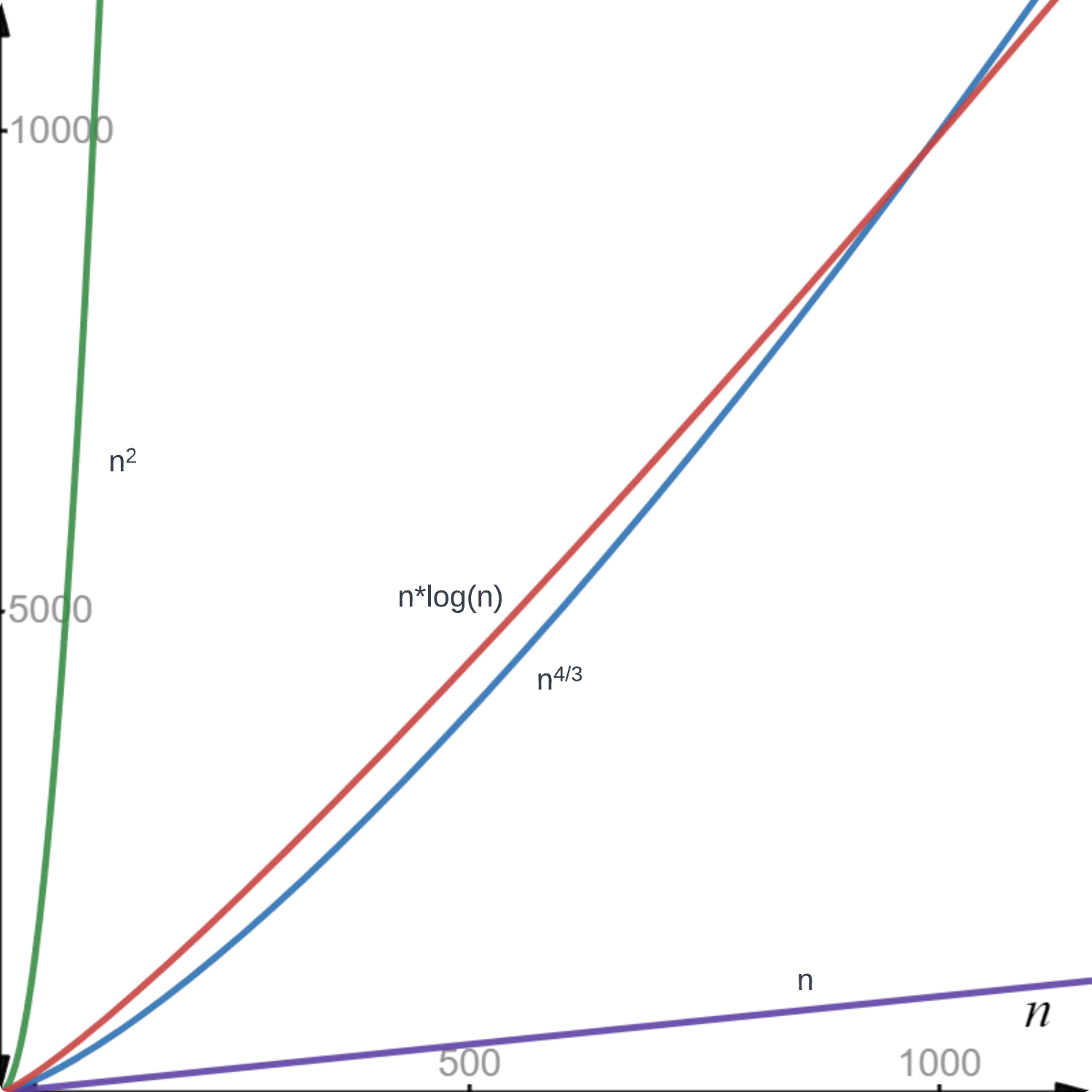
Wegen $\Omega(n\ log\ n)$ interessieren wir uns für die Intervalle:

• $n\ log\ n \leq c3 \leq n^{1.3}$

• $n\ log\ n \leq n^{1.3} \leq c3 \leq n^2$

Die Ausführung des Tests zeigt, dass die Aufrufanzahl von $c3$ bei großen $n$ unterhalb $n^{1.3}$ oder zwischen $n^{1.3}$ und $n^2$ liegt:

It appears that the time required to sort $n$ elements is proportional to $n^{1.226}$.⁴ [📖She59, p. 31]

Laufzeitanalyse

Für die nachfolgenden Betrachtungen sei eine Eingabegröße $n = 2^p$ gegeben. Die Inkremente $h$ entsprechen der über die Implementierung vorgegebenen Folge $h$ mit

$h_t = \frac{n}{2}, h_{t-1} = \frac{n}{4}, \dots, h_1 = 1$

Für die Analyse ist die Shellsort-Implementierung in Listing 3 gegeben.

Listing 3: Implementierung des Shellsort-Algorithmus.

public static int[] sort(int[] arr) {

    int n = arr.length;
    int delta = n/2;
    int min;
    int j;

    while (delta > 0) { // c1

        for (int i = delta; i < arr.length; i++) {

            // c2

            min = arr[i];
            j = i;

            while (j - delta >= 0 && min < arr[j - delta]) {

                // c3;

                arr[j] = arr[j - delta];
                j -= delta;
            }
            arr[j] = min;
        }

        delta = delta / 2;

    }
    return arr;
}

Im Folgenden betrachten wir die Anzahl für die im Code durch Kommentare markierten Stellen $c1$ in Zeile 8, $c2$ in Zeile 12 und $c3$ in Zeile 19.

Für eine erste worst-case-Analyse ist ein Feld der Länge $16$ gegeben, in absteigender Reihenfolge sortiert (s. Abbildung 2):

^{Figure 2 Die für die Laufzeitabschätzung verwendete Eingabefolge 16..1.}

Ganz offensichtlich gilt für c3, dass es $lg(n)$-mal aufgerufen wird⁵. c2 befindet sich im Block der durch die in Zeile 11 definierten Zählschleife.

Der Startwert für i ist in jedem Durchgang des Blocks $c1$ der aktuelle Wert von delta ⁶, und läuft jeweils bis $n - 1$.

In einem kompletten Durchlauf der Schleife entspricht die Anzahl der Aufrufe von $c2$ also

$(n - 1) - delta + 1 = n - delta$

info

Hinweis: Für das Beispiel betrachten wir der Einfachheit halber Feldlängen der Form $2^p$. Für den allgemeinen Fall gilt für die Anzahl der Aufrufe von $c2$:

$\sum_{i=1}^{\lfloor lg(n) \rfloor} n - \lfloor \frac{n}{2^i} \rfloor = n * lg(n) - \sum_{i=1}^{\lfloor lg(n) \rfloor} \lfloor \frac{n}{2^i} \rfloor$

Für die Gesamtzahl der Aufrufe von $c2$ ergibt sich somit unter Berücksichtigung von $c1$

$\sum_{i=1}^{lg(n)} n - \frac{n}{2^{i-1}}$

was nach Auflösen

$n * lg(n) - n + 1$

entspricht, und für unser Beispiel

$16 * lg(16) - 16 + 1 = 49$

ist.

info

Die Aufrufzahlen für $c2$ für verschiedene $n$. Schlüsselvergleiche finden erst später statt. Mit $n > 2156$ wächst $O(n^\frac{4}{3})$ schneller als $c2$ und mit $n >= 982$ schneller als $O(n\ log\ n)$.

n	c2	$O(n^{1.1})$	$O(n^{1.3})$	$O(n\ log\ n)$	$O(n^2)$
8	17	9	14	24	64
16	49	21	36	64	256
32	129	45	90	160	1024
64	321	97	222	384	4096
128	769	207	548	896	16.384
256	1793	445	1351	2048	65.536
1024	9217	2048	8192	10240	1.048.576
2156	21.565	4.645,29	21.564,69	23.875,84	4.648.336
2157	21.576	4.647,66	21.577,70	23.888,36	4.652.649
2158	21.586	4.650,03	21.590,70	23.900,88	4.656.964
...	...	...	...	...	...
10.000	120.005	25.118	158.489	132.877	1.0E8
100.000	1.500.006	316.227	3.162.277	1.660.964	1.0E10
200.000	3.200.006	677.849	7.786.440	3.521.928	4.0E10
500.000	8.500.007	1.857.235	2.56..E7	9.465.784	2.5E11
1.000.000	18.000.007	3.981.071	6.30..E7	1.99..E7	1.0E12

In der while-Schleife in Zeile 17 findet die eigentliche Arbeit des Algorithmus statt: Es wird überprüft, ob $delta$-entfernte Elemente in aufsteigender Reihenfolge sortiert angeordnet sind.

Ist das nicht der Fall, werden die Elemente an den Stellen $j$ und $j - delta$ ausgetauscht, bis die $h$-Folge sortiert ist.
Für den ersten Durchgang des Algorithmus an dieser Stelle mit $h_4 = 8$ ergibt sich somit die in Abbildung 3 dargestellte Reihenfolge der Schlüssel:

^{Figure 3 Nach dem ersten Durchgang sind die Schlüssel in den Abständen h₄ = 8 sortiert, es ergeben sich zwei sortierte Teilfolgen der Länge 8.}

Die weiteren Durchgänge des Algorithmus sortieren das Feld entsprechend der Größe $h$: Es sind danach jeweils Schlüssel mit den Abständen $4$ (Abbildung 4 und $2$ (Abbildung 5) sortiert; im letzten Schritt dann vollständig (Abbildung 6):

^{Figure 4 Die Sortierung für h₃ = 4, es sind 4 Folgen deren Schlüssel jeweils den Abstand 4 zueinander haben.}

^{Figure 5 Im vorletzten Sortierschritt sind 8 Folgen der Länge 2 sortiert.}

^{Figure 6 Der letzte Durchgang des Algorithmus vergleicht Schlüssel mit Distanzfolgen der Länge 1, also direkt benachbarte Schlüssel.}

Für die Berechnung der Anzahl der Aufrufe von $c3$ stellt man fest, das in diesem Fall in jedem Schritt immer 2 Elemente, die eine Distanz von $h_s$ aufweisen, falsch sortiert sind.

Der Algorithmus tauscht daraufhin in jedem Durchgang alle Schlüssel untereinander aus, die er über min < arr[j-delta] miteinander vergleicht, was folglich die maximale Anzahl von Schlüsselvertauschungen in dieser vergleichsbasierten Implementierung für ein Feld der Größe $n$ ergibt, nämlich $\frac{n}{2}$. Insgesamt finden dadurch für $c3$

$lg(n) * \frac{n}{2}$

Aufrufe statt.

Mit der Anzahl der berechneten Aufrufe $c1, c2, c3$ ergibt sich somit für die Laufzeit $T(n)$ für diesen Fall

$lg(n) + n * lg(n) - n + 1 + lg(n) * \frac{n}{2}$

und zusammengefasst

$f(n) = \frac{3}{2} * n * lg(n) + lg(n) - n + 1$

was nach Einsetzen zu

$lg(16) + 16 * lg(16) - 16 + 1 + lg(16) * \frac{16}{2} = 85$

Aufrufen für unser Beispiel führt.

Nachweis der Komplexitätsklasse

Um $O$ zu ermitteln, werden nun alle Konstanten der Funktion

$f(n) = \frac{3}{2} * n * lg(n) + lg(n) - n + 1$

eliminiert, und der "dominante" Summand in Abhängigkeit von $n$ betrachtet, der in diesem Fall $lg(n) * n$ ist.

Wir vermuten ein $N-log-N$-Wachstum⁷ (vgl. [📖OW17a, p. 5]), und wollen nun zeigen, dass $T(n)$ in $O(n\ log\ n)$ liegt.
Hierfür müssen wir ein geeignetes $c$ und ein $n_0$ finden, so dass gilt:

$f \in O(n\ log\ n): \leftrightarrow \exists n_0 \in \mathbb{N}, c \in \mathbb{R}, c > 0: \forall n \geq n_0: f(n) \leq c * n*lg(n)$

(vgl. [📖GD18a, p. 11]).

Zu zeigen ist

$\frac{3}{2} * n * lg(n) + lg(n) - n + 1 \leq c * n * lg(n)$

Wir wählen für $n_0 = 1$ und $c = \frac{3}{2}$, denn es gilt sicher

$\forall n \geq n_0: \frac{3}{2} * n * lg(n) \leq \frac{3}{2} * n * lg(n)$.

Ausserdem gilt stets $\forall n \in \mathbb{N}: lg(n) < n$, woraus $lg(n) - n < 0$ folgt, und damit auch $lg(n) - n + 1 \leq 0$.

Insgesamt gilt also

$n_0 = 1, c = \frac{3}{2}: \forall n \geq n_0: \frac{3}{2} * n * lg(n) + lg(n) - n + 1 \leq c * n * lg(n)$

womit $f = O(n * log(n))$ gezeigt ist. ◻

Worst-Case-Analyse

Unter der Annahme, dass ein in umgekehrter Reihenfolge sortiertes Feld zu einer Laufzeit von $O(n^2)$ bei dem Shellsort-Algorithmus führt, konnten wir mit dem in dem vorherigen Abschnitt gewählten Parametern nur eine Laufzeit von $O(n\ log\ n)$ nachweisen.
Tatsächlich stellt der Anwendungsfall nicht den worst-case für den Algorithmus dar, da ja gerade diese Form von Sortierreihenfolge dem Algorithmus die Vorsortierung der $h$-Folgen ermöglicht:

The idea underlying Shellsort is that moving elements of A long distances at each swap in the early stages, then shorter distances later, may reduce this $O(n^2)$ bound. [📖Pra72, p. 3]

Es gilt also, die Vorsortierung auszuhebeln.
Für Insertion-Sort ist die Laufzeit im worst-case $O(n^2)$ (vgl. [📖OW17b, p. 87]). Da Shellsort mindestens im letzten Schritt diese Sortiermethode auf Distanzfolgen der Länge $1$ anwendet, muss der Algorithmus eine Folge als Eingabe erhalten, die durch die ersten $lg(n) - 1$-Durchgänge (mit $h_s = 2^{s - 1}, 1 \leq s < lg(n)$) keine Änderungen erfährt, um dann im allerletzten Schritt auf einen Schlag sortiert wird, was maximal $\frac{n}{2}$ Inversionen⁸ bedeutet, und damit ebenso viele Vertauschungen (zuzüglich der benötigten Verschiebe-Operationen).
Hierzu kann wie im vorherigen Beispiel für $n=16$ ein Feld mit folgender Schlüsselanordnung verwendet werden: Felder mit geradem Index enthalten kleinere Schlüssel als Felder mit ungeradem Index. Hier gilt für alle Elemente aus dem Feld $A$:

$\forall i, j \in \mathbb{N}_{[0, n - 1]}, 2 \mid i, 2 \nmid j: A[i] < A[j] \land A[i] < A[i + 1] \land A[j] < A[j +1]$

Abbildung 7 veranschaulicht die Anordnung.

^{Figure 7 Eine worst-case Schlüsselfolge für Shellsort. Felder mit geradem Index enthalten kleinere Schlüssel als Felder mit ungeradem Index.}

Markiert sind die direkt benachbarten Felder, die eine Inversion aufweisen, die im letzten Schritt des Algorithmus eine bzw. mehrere Verschiebungen bedingen.
In den vorherigen Schritten - also bei den Durchgängen mit Distanzfolgen $h_s > 1$ - findet der Algorithmus jeweils Schlüssel in korrekter Sortierreihenfolge vor.

Mit $h_4 = 8$ werden die Felder $A[0..7]$ mit den Feldern $A[8..15]$ verglichen - hier gilt in jedem Fall, dass die Schlüssel $A[i] < A[j] (\forall i < j, j - i = 8)$ sind.

Auch im darauffolgenden Durchgang ($h_3 = 4, j - i = 4$) finden keine Verschiebungen statt, da keine Inversion gefunden wird. Erst im letzten Schritt, in dem direkt benachbarte Elemente miteinander verglichen werden, werden die Inversionen ermittelt und die Verschiebung der Elemente findet statt (s. Abbildung 8.

^{Figure 8 Für die worst-case Schlüsselfolge werden im letzten Schritt 7 Inversionen festgestellt. Jede dieser Fehlstellung bedingt eine Verschiebung um die angegebene Anzahl von Positionen.}

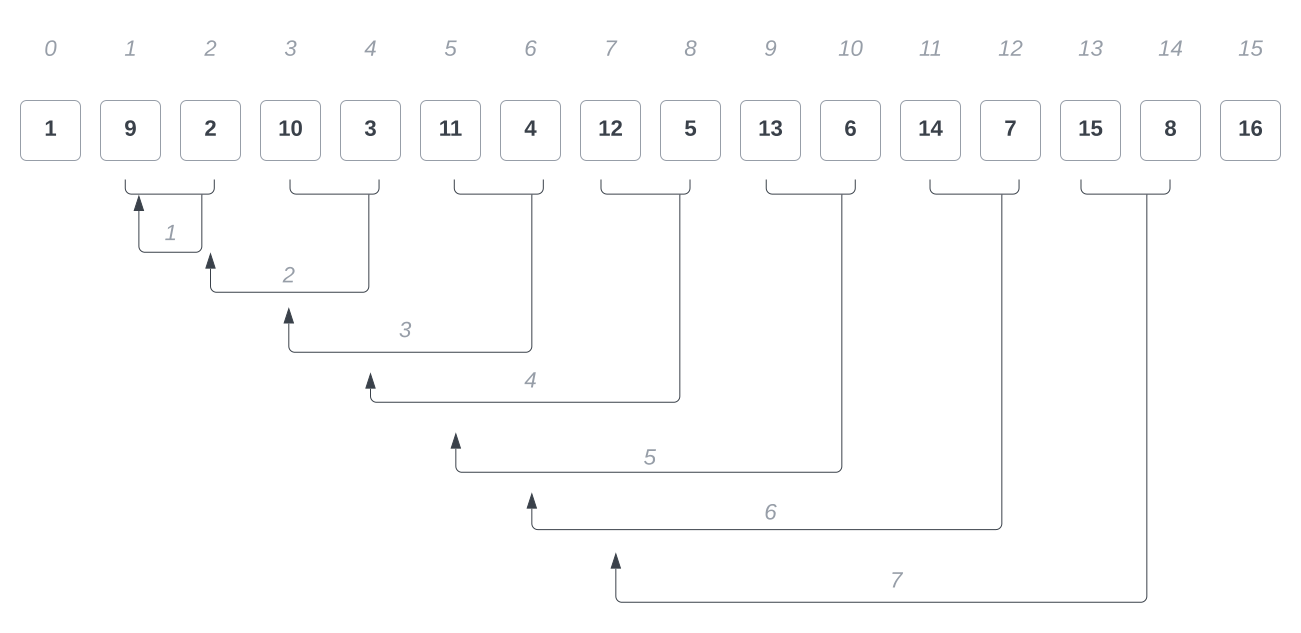
In diesem Fall wird $c3$ insgesamt $32$ mal aufgerufen.

Da jeweils zwei Schlüssel bereits korrekt sortiert sind ($A[0]$ und $A[n-1]$) existieren noch $\frac{n}{2} - 1$ Inversionen. Jede Inversion erzwingt eine Verschiebung des größten Elements um $\frac{i}{2}$ Positionen nach links.

Für die Berechnung der Laufzeitkomplexität ergibt sich somit der Term

$\sum_{i=1}^{\frac{n}{2} - 1} i = \frac{\frac{n}{2}(\frac{n}{2} - 1)}{2} = \frac{n^2 - 2n}{8}$

und unter Berücksichtigung der Terme für $c1$, $c2$, $c3$ die Funktion

$f(n) = lg(n) + n * lg(n) - n + 1 + \frac{n^2 - 2n}{8}$

was zu einer Laufzeitabschätzung von $O(n^2)$ führt.

---

1. mit $n =$ Länge des zu sortierenden Feldes. Im folgenden $lg$ für $log_2$.↩
2. vgl. [📖Knu97c, p. 84]↩
3. Knuth bezieht sich hier auf die Arbeit von Papernov und Stasevich ([📖PS65]). Weitere Verweise auf Laufzeiten in Abhängigkeit von $n$ und $h$ fasst übersichtlich der Wikipedia-Artikel zusammen: https://en.wikipedia.org/wiki/Shellsort (abgerufen 23.01.2024).↩
4. Shell führt in seinem Paper keinen Beweis auf. Er stützt seine Behauptung auf Messungen, die er selber in Tests durchgeführt hat: "[...] an analytical determination of the expected speed has eluded the writer. However, experimental use has established its speed characteristics." (ebenda)↩
5. hier wie im folgenden ohne Betrachtung der Schleifenbedingung, die an dieser Stelle insgesamt $lg(n) + 1$-mal aufgerufen wird↩
6. ${8, 4, 2, 1}$ für das gegebene Beispiel↩
7. mit $O(log\ n)$ bzw $O(n\ log\ n)$ nehmen wir für die $O$-Notation wieder die in der Fachliteratur gebräuchlichere Schreibweise auf. Sowohl Güting und Dieker als auch Ottmann und Widmayer weisen in [📖GD18a, p. 15] bzw. [📖OW17a, p. 5] darauf hin, dass die Angabe der Basis keine Rolle spielt, da sich Logarithmen mit verschiedenen Basen ohnehin nur durch einen konstanten Faktor unterscheiden (es gilt $log_a(x) = \frac{log_b(x)}{log_b(a)}$).↩
8. in diesem Zusammenhang bedeutet Inversion: Fehlstellung (vgl. [📖OW17b, p. 87])↩